|
|
在实现很多效果时, 我们需要各种各种的噪声, 这里来简单小结下常用的噪声算法.
这里假设我们现在已经有了一个生成随机数的random()方法, 生成伪随机数的方法有很多种, 这里不再赘述.
对于我们来说, 生成存粹的白噪声非常简单, 只需要应用随机数就可以了.
但是自然界中的噪声大多是连续的, 很多情况下我们希望得到的噪声也应该是连续的. 下面就来简单说明下常用的生成连续噪声的算法.
一、Perlin噪声
(A) Perlin值噪声
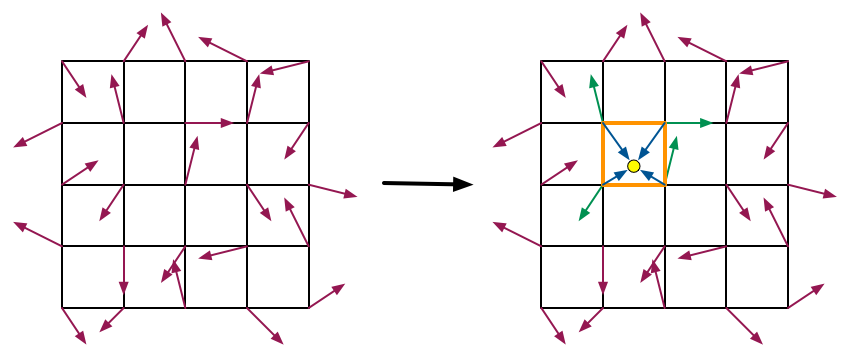
Perlin噪声的思路是将整个空间区域划分为一个个小的格子, 在每个格子顶点上随机取值, 在格子顶点外的区域, 通过将周围顶点的值进行混合来得到基于值的噪声.
比如在二维情况下, 将整个区域划分成小正方形, 每个正方形顶点随机得到一个值. 对于区域内任意一点, 可以得到相对顶点的偏移 st , 为了使相邻格子间的值更加连续, 这里将偏移值通过多项式进行平滑处理:
f(u) = 3u^2-2u^3\\ 这种处理等价于shader中 smoothstep()的实现.
实现的代码大致如下:
uniform vec2 u_resolution;
// 2D Random
float random (in vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))
* 43758.5453123);
}
// 2D Noise based on Morgan McGuire @morgan3d
// https://www.shadertoy.com/view/4dS3Wd
float noise (in vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
// 获取每个格子的顶点
float a = random(i);
float b = random(i + vec2(1.0, 0.0));
float c = random(i + vec2(0.0, 1.0));
float d = random(i + vec2(1.0, 1.0));
// 平滑插值
// Cubic Hermine Curve. Same as SmoothStep()
vec2 u = f*f*(3.0-2.0*f);
// u = smoothstep(0.,1.,f);
// 将四个角的值线性插值
return mix(a, b, u.x) +
(c - a)* u.y * (1.0 - u.x) +
(d - b) * u.x * u.y;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
// 将区域划分成5X5格子
vec2 pos = vec2(st*5.0);
// 噪声算法
float n = noise(pos);
gl_FragColor = vec4(vec3(n), 1.0);
}

(B) Perlin梯度噪声
上面的方式得到的噪声, 有一个很大的缺陷. 就是虽然已经进行了平滑处理, 得到的噪声图还是有明显的块状感. 因此对此的改进是将基于值的噪声改为基于梯度的噪声.
基于梯度的噪声, 在每个顶点并非直接生成值, 而是生成一个梯度向量. 这样在内部插值时, 先得到求值点到周围顶点的向量, 再将向量之间求点积并取和.
大致代码为:
uniform vec2 u_resolution;
vec2 random2(vec2 st){
st = vec2( dot(st,vec2(127.1,311.7)),
dot(st,vec2(269.5,183.3)) );
return -1.0 + 2.0*fract(sin(st)*43758.5453123);
}
// Gradient Noise by Inigo Quilez - iq/2013
// https://www.shadertoy.com/view/XdXGW8
float noise(vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
vec2 u = f*f*(3.0-2.0*f);
return mix( mix( dot( random2(i + vec2(0.0,0.0) ), f - vec2(0.0,0.0) ),
dot( random2(i + vec2(1.0,0.0) ), f - vec2(1.0,0.0) ), u.x),
mix( dot( random2(i + vec2(0.0,1.0) ), f - vec2(0.0,1.0) ),
dot( random2(i + vec2(1.0,1.0) ), f - vec2(1.0,1.0) ), u.x), u.y);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.0);
vec2 pos = vec2(st*10.0);
color = vec3( noise(pos)*.5+.5 );
gl_FragColor = vec4(color,1.0);
}

(C) Perlin梯度噪声的改进
Perlin本人在梯度噪声基础上, 提出的一些优化. [https://mrl.cs.nyu.edu/~perlin/paper445.pdf]包括这样两点:
(1) 改进平滑曲线, 使用五次多项式:
f(u) = 6u^5 - 15u^4 + 10u^3\\
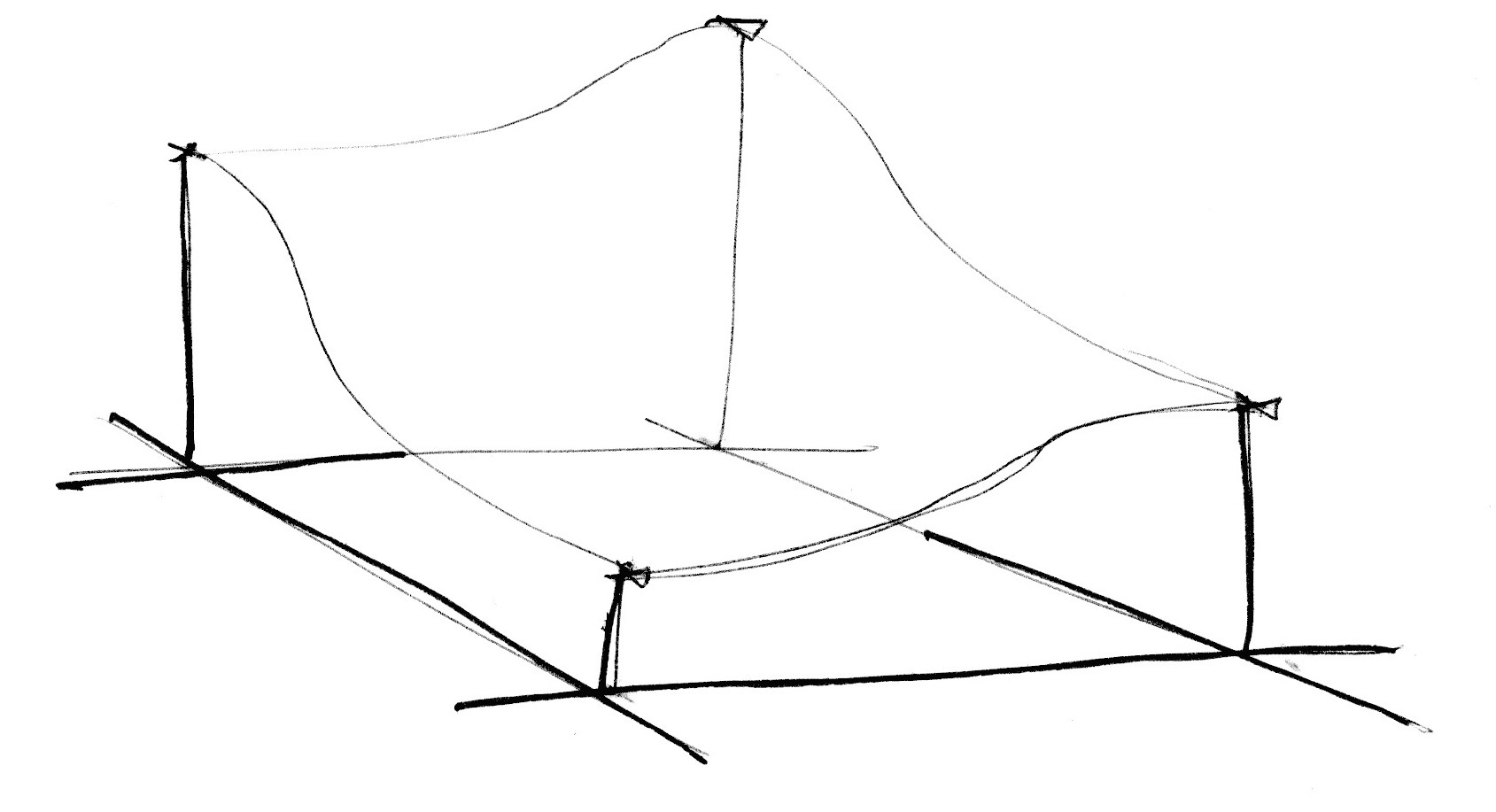
(2) 每个顶点的梯度向量不再是从随机值得到, 而是预设一些值, 然后从中随机挑选. 比如在三维下预设的顶点梯度向量为12条边指向立方体中心的向量:
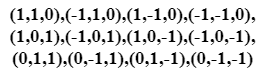
这里用12作为模取余数, 如果不想用12而用16作为模, 可以再加上这4个构成正四面体的点, 不影响最终的效果:
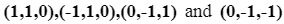
(D) Simplex噪声
Perlin对梯度噪声的改进, 用来优化运行效率 http://staffwww.itn.liu.se/~stegu/simplexnoise/simplexnoise.pdf.
Simplex/单形指在N维下, N+1个点即可构成凸多面体.
比如在二维下, 平面可以看成正三角形的拼接. 在三维下, 空间可以看成正四面体的拼接.
这样就可以减少我们插值时所需要的顶点的个数, 加快运行速度, 在高维度下有显著的效果, 运行时间复杂度由 O(2^N) 降低为 O(N^2) .
为了计算方便, 我们需要在单纯形网格和正方形网格形之间做坐标变换.
在二维平面上, 网格形和单形可以通过偏斜操作来实现, 就是将正方形网格沿对角线挤压, 即可形成单形. 在三维甚至高维空间上也是一样, 沿着主对角线挤压, 只是拼接的过程会比较复杂.
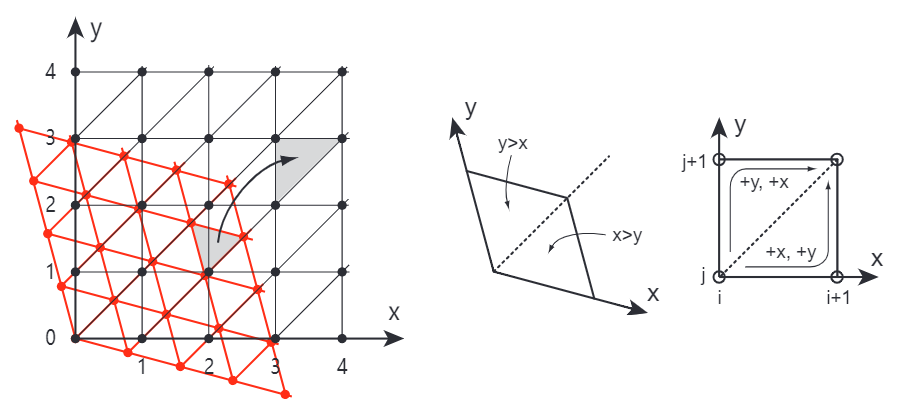
我们计算Simplex噪声的过程分为这样几步:
(1) 得到随机点, 假设现在这些点处于单纯形网格上.
(2) 将单形网格下坐标变换为正方形网格下坐标. 这一步的目的是方便得到网格中每个顶点的索引, 而且变换成正方形网格坐标后. 根据网格内的xy值相对大小, 就可以知道当前单形网格是两块中的哪一块.
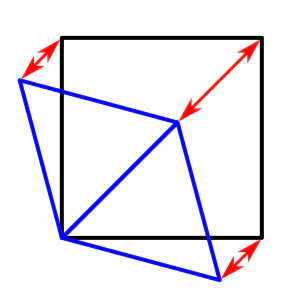
变换的公式为:
F = \frac{\sqrt{3} - 1}{2}\\ x' = x + (x+y) * F\\ y ' = y + (x+y) * F
在N维空间下的的计算方式为:
F = \frac{\sqrt{N+1} - 1}{N}\\ x' = x + (x+y + z + \dots) * F\\ \dots
(3) 得到每个顶点梯度值, 这一步可以是生成随机数, 或者根据索引从向量表中获取.
(4) 将左下角顶点变换回单形网格下坐标. 这里的目的是为了后面计算点在单形内到每个顶点的相对向量, 来计算噪声值.
这里的变换方式其实就是上面一步变换的逆运算:
G = \frac{3 - \sqrt{3} }{6}\\ x = x' - (x'+y') * G\\ y = y' - (x'+y') * G
(5) 噪声值计算, 这部分计算方式和之前的梯度噪声一样, 不同的地方在于每个顶点的影响范围较小一些, 这样单形内的每个点只会受到周围三个顶点的影响:
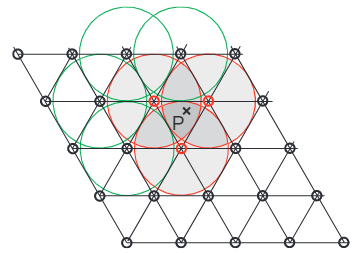
实现代码大致为:
uniform vec2 u_resolution;
vec3 mod289(vec3 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }
vec2 mod289(vec2 x) { return x - floor(x * (1.0 / 289.0)) * 289.0; }
vec3 permute(vec3 x) { return mod289(((x*34.0)+1.0)*x); }
float snoise(vec2 v) {
const vec4 C = vec4(0.211324865405187, // (3.0-sqrt(3.0))/6.0
0.366025403784439, // 0.5*(sqrt(3.0)-1.0)
-0.577350269189626, // -1.0 + 2.0 * C.x
0.024390243902439); // 1.0 / 41.0
vec2 i = floor(v + dot(v, C.yy) );
vec2 x0 = v - i + dot(i, C.xx);
vec2 i1;
i1 = (x0.x > x0.y) ? vec2(1.0, 0.0) : vec2(0.0, 1.0);
vec4 x12 = x0.xyxy + C.xxzz;
x12.xy -= i1;
i = mod289(i); // Avoid truncation effects in permutation
vec3 p = permute( permute( i.y + vec3(0.0, i1.y, 1.0 ))
+ i.x + vec3(0.0, i1.x, 1.0 ));
vec3 m = max(0.5 - vec3(dot(x0,x0), dot(x12.xy,x12.xy), dot(x12.zw,x12.zw)), 0.0);
m = m*m ;
m = m*m ;
vec3 x = 2.0 * fract(p * C.www) - 1.0;
vec3 h = abs(x) - 0.5;
vec3 ox = floor(x + 0.5);
vec3 a0 = x - ox;
m *= 1.79284291400159 - 0.85373472095314 * ( a0*a0 + h*h );
vec3 g;
g.x = a0.x * x0.x + h.x * x0.y;
g.yz = a0.yz * x12.xz + h.yz * x12.yw;
return 130.0 * dot(m, g);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.0);
vec2 pos = vec2(st*10.);
color = vec3(snoise(pos)*0.5 + 0.5);
gl_FragColor = vec4(color,1.0);
}
借助这些噪声算法, 可以产生一些非常漂亮的图案, 下面就是一个通过扭曲空间实现的效果:
uniform vec2 u_resolution;
float random (in vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))
* 43758.5453123);
}
// Value noise by Inigo Quilez - iq/2013
// https://www.shadertoy.com/view/lsf3WH
float noise(vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
vec2 u = f*f*(3.0-2.0*f);
return mix( mix( random( i + vec2(0.0,0.0) ),
random( i + vec2(1.0,0.0) ), u.x),
mix( random( i + vec2(0.0,1.0) ),
random( i + vec2(1.0,1.0) ), u.x), u.y);
}
// 旋转矩阵
mat2 rotate2d(float angle){
return mat2(cos(angle),-sin(angle),
sin(angle),cos(angle));
}
float lines(in vec2 pos, float b){
float scale = 10.0;
pos *= scale;
return smoothstep(0.0,
.5+b*.5,
abs((sin(pos.x*3.1415)+b*2.0))*.5);
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.y *= u_resolution.y/u_resolution.x;
vec2 pos = st.yx*vec2(10.,3.);
float pattern = pos.x;
// Add noise
pos = rotate2d( noise(pos) ) * pos;
// Draw lines
pattern = lines(pos,.5);
gl_FragColor = vec4(vec3(pattern),1.0);
}

二、Worley噪声
(A) Voronoi Diagram
很多情况下, 我们期望得到类似网格状的噪声, 作为程序化纹理使用.
一种思路是输入一些特征点, 在产生噪声时, 计算当前点到每个特征点的距离, 选择距离最近的那个点, 作为当前的特征点, 进行一些处理, 这种由特征点来划分区域的方式叫做Voronoi Diagram:

uniform vec2 u_resolution;
uniform vec2 u_mouse;
uniform float u_time;
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(.0);
// Cell positions
vec2 point[5];
point[0] = vec2(0.83,0.75);
point[1] = vec2(0.60,0.07);
point[2] = vec2(0.28,0.64);
point[3] = vec2(0.31,0.26);
point[4] = u_mouse/u_resolution;
float m_dist = 1.; // minimum distance
vec2 m_point; // minimum position
// Iterate through the points positions
for (int i = 0; i < 5; i++) {
float dist = distance(st, point);
if ( dist < m_dist ) {
// Keep the closer distance
m_dist = dist;
// Kepp the position of the closer point
m_point = point;
}
}
// Add distance field to closest point center
color += m_dist*2.;
// tint acording the closest point position
color.rg = m_point;
// Show isolines
color -= abs(sin(80.0*m_dist))*0.07;
// Draw point center
color += 1.-step(.02, m_dist);
gl_FragColor = vec4(color,1.0);
}但是, 对于比较大的平面, 要预设所有的特征点, 并循环和所有特征点计算距离, 是不现实的.
(B) Worley噪声
Worley提出一种流行的程序化方案http://www.rhythmiccanvas.com/research/papers/worley.pdf, 将整个平面划分成许多正方形网格(前面我们一直在用的噪声技巧), 每个网格内随机得到一个特征点.
这样每个点, 只需要在周围的九个网格内循环寻找到特征点的最小距离即可:
产生的效果:

通过Worley噪声, 再将空间进行切分, 并根据时间做一些参数变换, 可以得到一些美丽的程序化纹理:

三、分形噪声/fBM
(A) 正弦波叠加
有了一维值的平滑噪声是不够的, 很多时候, 我们需要更多的细节.
通过将噪声值进行叠加, 可以产生更多的细节.
正弦波是生活中最常见的波, 有两个重要属性, 振幅(amplitude)和频率(frequency). 一个简单的正弦波如下:
float amplitude = 1.;
float frequency = 1.;
y = amplitude * sin(x * frequency);通过改变振幅和频率的大小, 我们可以控制波的属性.
现在, 我们可以将不同频率和振幅的波进行叠加:
float amplitude = 1.;
float frequency = 1.;
y = sin(x * frequency);
float t = 0.01*(-u_time*130.0);
y += sin(x*frequency*2.1 + t)*4.5;
y += sin(x*frequency*1.72 + t*1.121)*4.0;
y += sin(x*frequency*2.221 + t*0.437)*5.0;
y += sin(x*frequency*3.1122+ t*4.269)*2.5;
y *= amplitude*0.06;
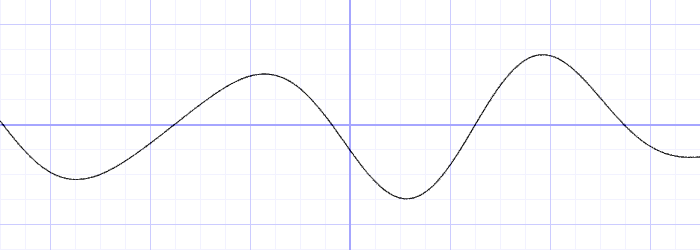
(B) 分形噪声
Perlin 噪声跟正弦波很相似,我们也可以使用频率和振幅的概念,将不同频率的 perlin 噪声叠加。
在这里, 我们用八度指代叠加的波的个数。在音乐理论中,每个八度(octaves)表示将频率加倍或者减半。
通过在循环(循环次数为octaves,一次循环为一个八度)中叠加噪声,并以一定的倍数(lacunarity,间隙度)连续升高频率,同时以一定的比例(gain,增益)降低噪声的振幅,最终的结果会有更好的细节。这项技术叫“分形布朗运动(fractal Brownian Motion)”(fBM),或者“分形噪声(fractal noise):
注意,随着我们一个八度接一个八度地往上叠加,曲线看起来有越来越多的细节,同时,自相似性也越来越明显。如果你放大看看,曲线的局部和整体看起来很相似,并且,任选两段不同的部分看起来也多少有些相似。这是一个数学上的分形的重要性质,我们在上面的循环中模拟了这个性质。我们不是要创造一个真的分形,因为我们在几次循环之后就不再往上叠加了,但理论上说,如果我们一直继续这个循环,不断地往上叠加噪声,就会得到一个真正的数学意义上的分形。在计算机图形领域,我们能处理的细节总是有极限的,比如物体比一个像素还小的时候,所以没有必要不断地往上叠加来制造分形的形态。有时候我们确实需要叠加很多次,但不必叠加无限次。
uniform vec2 u_resolution;
float random (in vec2 st) {
return fract(sin(dot(st.xy,
vec2(12.9898,78.233)))*
43758.5453123);
}
// Based on Morgan McGuire @morgan3d
// https://www.shadertoy.com/view/4dS3Wd
float noise (in vec2 st) {
vec2 i = floor(st);
vec2 f = fract(st);
// Four corners in 2D of a tile
float a = random(i);
float b = random(i + vec2(1.0, 0.0));
float c = random(i + vec2(0.0, 1.0));
float d = random(i + vec2(1.0, 1.0));
vec2 u = f * f * (3.0 - 2.0 * f);
return mix(a, b, u.x) +
(c - a)* u.y * (1.0 - u.x) +
(d - b) * u.x * u.y;
}
#define OCTAVES 6
float fbm (in vec2 st) {
// Initial values
float value = 0.0;
float amplitude = .5;
float frequency = 0.;
//
// Loop of octaves
for (int i = 0; i < OCTAVES; i++) {
value += amplitude * noise(st);
st *= 2.;
amplitude *= .5;
}
return value;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy;
st.x *= u_resolution.x/u_resolution.y;
vec3 color = vec3(0.0);
color += fbm(st*3.0);
gl_FragColor = vec4(color,1.0);
}

当然,我们这里的叠加,也是不限于使用 Perlin 噪声的,Worely噪声也是可以使用这种方式进行叠加的。我们还可以将Perling噪声和Worely噪声进行叠加,形成Perlin-Worely噪声,这种噪声常常用于模拟云的形状。

Perlin-Worley噪声
(C) fBM的应用
分形噪声被广泛地应用在程序化风景中, 比如模拟山脉, fBM 的自相似性可以很好地模拟山脉形成过程中的不同尺度上的自相似特征 https://www.iquilezles.org/www/articles/morenoise/morenoise.htm .

fBM创建的山脉
将噪声的值都取绝对值, 这样值叠加可以产生尖锐的湍流(turbulence)效果:
for (int i = 0; i < OCTAVES; i++) {
value += amplitude * abs(snoise(st));
st *= 2.;
amplitude *= .5;
}

类似的做法是将值反过来, 这样将山谷变成山脊:
n = abs(n); // create creases
n = offset - n; // invert so creases are at top
n = n * n; // sharpen creases

fBM的另外一种形式, 是将得到的噪声值相乘, 这样可以形成&#34;多重分形&#34;, 创造出一些有趣的东西.
除了用作噪声值外, fBM还可以用来扭曲空间, 创建烟雾, 流体等效果, 在前面我们就提到用 perlin 噪声扭曲空间的效果, 使用fBM可以产生更加光滑自然的效果 http://www.iquilezles.org/www/articles/warp/warp.htm.
uniform vec2 u_resolution;
uniform float u_time;
float random (in vec2 _st) {
return fract(sin(dot(_st.xy,
vec2(12.9898,78.233)))*
43758.5453123);
}
// Based on Morgan McGuire @morgan3d
// https://www.shadertoy.com/view/4dS3Wd
float noise (in vec2 _st) {
vec2 i = floor(_st);
vec2 f = fract(_st);
// Four corners in 2D of a tile
float a = random(i);
float b = random(i + vec2(1.0, 0.0));
float c = random(i + vec2(0.0, 1.0));
float d = random(i + vec2(1.0, 1.0));
vec2 u = f * f * (3.0 - 2.0 * f);
return mix(a, b, u.x) +
(c - a)* u.y * (1.0 - u.x) +
(d - b) * u.x * u.y;
}
#define NUM_OCTAVES 5
float fbm ( in vec2 _st) {
float v = 0.0;
float a = 0.5;
vec2 shift = vec2(100.0);
// Rotate to reduce axial bias
mat2 rot = mat2(cos(0.5), sin(0.5),
-sin(0.5), cos(0.50));
for (int i = 0; i < NUM_OCTAVES; ++i) {
v += a * noise(_st);
_st = rot * _st * 2.0 + shift;
a *= 0.5;
}
return v;
}
void main() {
vec2 st = gl_FragCoord.xy/u_resolution.xy*3.;
// st += st * abs(sin(u_time*0.1)*3.0);
vec3 color = vec3(0.0);
vec2 q = vec2(0.);
q.x = fbm( st + 0.00*u_time);
q.y = fbm( st + vec2(1.0));
vec2 r = vec2(0.);
r.x = fbm( st + 1.0*q + vec2(1.7,9.2)+ 0.15*u_time );
r.y = fbm( st + 1.0*q + vec2(8.3,2.8)+ 0.126*u_time);
float f = fbm(st+r);
color = mix(vec3(0.101961,0.619608,0.666667),
vec3(0.666667,0.666667,0.498039),
clamp((f*f)*4.0,0.0,1.0));
color = mix(color,
vec3(0,0,0.164706),
clamp(length(q),0.0,1.0));
color = mix(color,
vec3(0.666667,1,1),
clamp(length(r.x),0.0,1.0));
gl_FragColor = vec4((f*f*f+.6*f*f+.5*f)*color,1.);
}

四、旋度噪声
(A) 散度和旋度
很多时候,我们希望得到无源(divergence free)向量场,用来模拟水流、雾的流动效果。因为在无源场中,流体都是不可压缩(incompressible)的,我们在生活中遇到的大部分流体,也是符合这个特征的。而Perilin噪声其实是不符合这个特征的,如果直接使用perlin噪声作为速度场使用,模拟粒子时就会出现某些地方闪烁的效果。所以我们使用 curl 运算处理,将 perlin 噪声转化成无源场噪声。
对于向量场:
\bm A (x,y,z) = (P(x,y,z),Q(x,y,z),R(x,y,z))\\
散度(divergence)的定义为:
div \bm A = \nabla \cdot \bm A = \frac{\partial P}{ \partial x} + \frac{\partial Q}{ \partial y} + \frac{\partial R}{ \partial z} \\
从物理意义上来说,散度表示流体的通量。散度为0表示是无源场,散度不为0是有源场。比如水流的速度场就是无源场,由电荷形成的电场就是有源场。
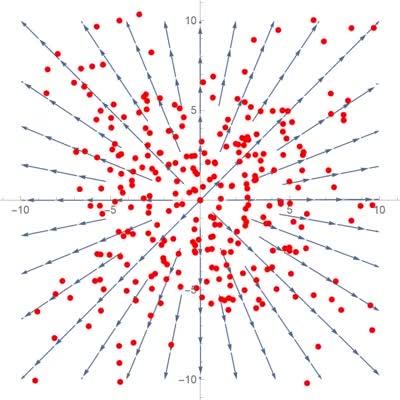
https://www.逍遥.com/video/1412783382170775552
旋度(curl)的定义为:
\bm {rot} \bm A = \nabla \times \bm A = \begin{vmatrix} \bm i & \bm j & \bm k \\ \frac{\partial }{ \partial x} &\frac{\partial }{ \partial y} & \frac{\partial }{ \partial z} \\ P& Q & R \end{vmatrix}\\ = \left (\frac{\partial R }{ \partial y} - \frac{\partial Q }{ \partial z} \right)\bm i + \left (\frac{\partial P }{ \partial z} - \frac{\partial R }{ \partial x} \right)\bm j + \left (\frac{\partial Q }{ \partial x} - \frac{\partial P }{ \partial y} \right)\bm k
从物理意义上来说,旋度表示一个向量场旋转的趋势:
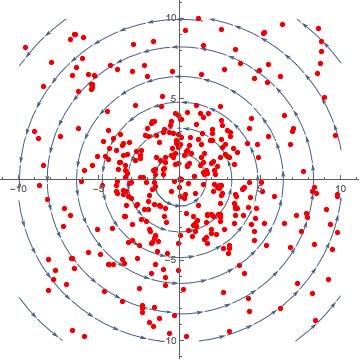
https://www.逍遥.com/video/1412789432794177536
对于任意的一个向量场,旋度总是无散的,也就是说,向量场旋度的散度总是0:
\nabla \cdot \nabla \times A \equiv 0\\
而我们的目标就是得到一个散度为0的无源场,因此我们通过这样的方法来实现:
先使用Perlin噪声得到一个随机的向量场,再对这个噪声向量场求旋度,就能得到散度为0的速度场了,下面是具体的方法。
(B) 2D旋度噪声
在2D情况下,旋度公式是这样的:
B(x,y) = (P(x,y),Q(x,y))\\ \nabla \times \bm B = \begin{vmatrix} \bm i & \bm j & \bm k \\ \frac{\partial }{ \partial x} &\frac{\partial }{ \partial y} & 0 \\ P& Q & 0 \end{vmatrix} = \left (\frac{\partial Q }{ \partial x} - \frac{\partial P }{ \partial y} \right)\bm k
这里得到的旋度其实是一个标量,因此我们这里只使用一个perin噪声函数 \psi ,并写成使用流体动力学中的流函数的形式:
v(x,y) = \left (\frac{\partial \psi }{ \partial y} ,- \frac{\partial \psi }{ \partial x} \right)\\
下面就是进行计算了,这里需要计算噪声值沿着 x,y 方向的变化率,直接使用简单的微分法计算即可。
下面是分别使用perlin噪声和使用旋度噪声作为速度场的粒子模拟效果:

(C) 3D旋度噪声
在3D场景下,我们就需要三个互相不相关的空间perlin噪声 \psi_1, \psi_2,\psi_3 了,同时计算的过程也会复杂很多:
v(x,y,z) = \left (\frac{\partial \psi_3 }{ \partial y} - \frac{\partial \psi_2 }{ \partial z} , \frac{\partial \psi_1 }{ \partial z} - \frac{\partial \psi_3 }{ \partial x} ,\frac{\partial \psi_2 }{ \partial x} - \frac{\partial \psi_1 }{ \partial y} \right)\\
计算的方式和2D情况下是一样的,都是通过微分的方式进行计算。
--END--
参考
The Book of Shaders
Simplex Noise(一)
凉虾:Perlin噪声与Simplex噪声笔记
http://platforma-kooperativa.org/media/uploads/curl_noise_slides.pdf
gwave:Del算符与梯度、散度、旋度与Laplacian
文章来源于网络,如有侵权,请联系我们小二删除,どうもで~す! |
|